Unit 3 Revision- Leap Frog Slides

Leap Frog PPT Slides Basic Relationships

Leap Frog PPT Slides Graphical & Numeric Relationships

Scribe Post 12/10/10

Click here to go to the blog post.

1999 FRQ Solutions

http://apcentral.collegeboard.com/apc/members/repository/sg_calculus_ab_99.pdf

Scribe Post 12/8/10

THE BEST BLOG POST EVER!!!!!1!!1

Unit 3 Assignment 7 & 8 Solutions

http://apcalculus.obrienfamily.sent.com/U3%20Assignments%20%237%20%26%208%20solutions.pdf

Scribe Post - December 6, 2010

Click HERE for the Google doc.

December 2 Blog Post

First, we started off class with our Quiz. OB was nice, and gave us extra time to do it, so we ran until 10:10.
After the Quiz was over, we pulled out the "1999 AP Calculus AB" Multiple Choice Questions (just the first five) that we worked on.

Then, we pulled up the "Exploration 8-3: Maximal Cylinder in a Cone Problem" and started it on our own. As usual, we worked through it for a while, before OB decided it was time for him to step in and help us work through the rest of it.

This Exploration was all about "Optimization." Optimization means you're looking for the best, worst, or optimal result of a problem. For our Exploration, we needed to find the Optimal Volume. We started out by making of a table relating radius, height, and Volume.



We filled in this chart by using the Volume of a Cylinder (). So, we have something "tres bizarre" here. The Maximum volume is actually up in the Area of 3. But we can't just take Nickname's word for it, and use 3 as our Optimal Height. We need to check other values that aren't just 1, 2, 3, or 4.
Then, we rewrote the Volume of a Cylinder Equation in terms of x, which resulted in . This is our "Primary Equation". We then found an equation for the relation to x and y. We can either look at this as a Number Pattern, or use point/slope to create a y=12-3x. Now that we have both of these equations, we can combine them to create our "Secondary Equation", so we just have an x: .
For the third part, we just used implicit differentiation, and got
Now we can just set V' equal to Zero, and find our answer for 4. Hopefully we all know how to simplify by now, so I won't write the steps. Our resulting Zeros were x=0, and x=-8/3. We can just take out Zero, from Context (we can't have x be zero, or our Volume is nonexistent), so our only resulting answer is x=-8/3! Ta-Da!

But, we have to check it in our Calclulators, so we graphed our Function, and made the Calculator find the Maximum. However, we're smarter than our silly calculators, because we can find the real answer, not just some rounded decimal approximation.

Now, we need to make sure that even through all of our Smart Moments, we need to answer the Question. So in summary, we should write something along the lines of:










And for future Reference, the thing that makes Optimization problems really hard isn't the Concept schtuff, it's the fact that they are the dreaded……………

So, we'll work on these for the next couple of days.

Here's Paul's Explanation of Optimization.

And at the End of Class, OB told us to make sure to tell everyone else that the Quiz was CRAZY hard, and our brains have turned to Jell-O.

Optimization Exploration Link

Optimization Exploration for today's class.

Scribe Post November 30, 2010

Here is the google doc to my scribe post.
Click here

(Update in google docs)

Leap Frog Game

Leap Frog Game 

• Have students arrange their game cards on their desks 
• After the first part of a statement is read using the Power Point presentation, students complete the statement by holding up the most complete correct answer 
• Students who answer incorrectly must remain in their seats 
• Students who answer correctly will proceed to the next available seat, “leap frogging” over the students who were incorrect 
• Play continues until a student returns to his/her original seat 

Rules: 

• All functions are continuous and twice differentiable. 
• Once a student holds up a card, they have committed and cannot change cards 

Relationships Game—Part One (Basic Relationships) 

• Uses the verbal cards (with “changes signs”) 
• Bonus questions have two correct answers and allow the students to leap frog two desks. A student must hold up both correct cards to be eligible to leap. 

Relationships Game—Part Two (Graphical and Numerical) 

• Uses the numerical cards 
• The functions represented by numerical tables are monotonic between data points 
• Game card values represent x values 
• Students hold up two cards to represent an interval 

Relationships Game—Part Three (Linear Motion) 

• Uses the verbal cards (with “equals zero”)

Scribe Post Tuesday 11/23/10

Click here for the scribe post from 11/23/10

Scribe Post Friday November 19, 2010

We started class with working on a problem that Mr. O'Brien had on his AP exam all those years ago. Back in that day they didn't use graphing calculators, so the problems were a little different. After working on this question for a few minutes Mr. O'Brien told us some about how our exam will be in May. Then, he continued by going over the problem on the board.

Steps to solve related rates word problems:
1) Find our what it is about, and draw a picture
2) Identifying variables and constants
3) Write equation(s) relating the variables
4) Differentiate LHS and RHS with respect to t
5) Solve by adding in variables

This struck the end of related rates and lead us into our next set of word problems.

The next set of word problems are for extreme values of functions. So, we started learning the Calculus we will need to do to solve this problems by doing a few example problems...

f(x)=-x^3+6x^2
on [-1,5]

f'(x) = -3x^2+12x
Where f'(x) = 0

0=-3x^2-12x

=-3x(x-4)

x = 0,4

Now we can plug these numbers back into the f(x) function and we get
f(0) = 0

f(4) = 32

So, The minimum is 0 because it is the lower of the two and the maximum is 32 because it is the higher.

We graphed this as well... however my computer is having problems posting images. I'll work on it and try to get these up for everyone soon.

Next, we did the same problem however with a limit of [-1,7].
What was interesting about this was that when we graphed this we could see that the graph starts to have a steady negative slope between the x values of 5 and 7, and this made it so the the absolute minimum changed quite a lot. This is easy to get a visual on geogebra, but again it won't let me upload the images onto the blog and therefore I will have to add this images later.

However, we can solve the minimum without a graph by plugging in 7 as x in the function. And.... f(7) = -49. Since this value is the lesser now it is apparent that -49 is the minimum.

When looking for extreme values of a function:
1) Locate places where the derivative of the function is 0 or undefined, and these are the critical points
2) Evaluate the function at these critical points
3) Evaluate the function at the end points
4) Pick out biggest and smallest and call these the extreme values.

An important note is that if derivatives change from (+) to (-) it is a max. And, if the derivative changes from a (-) to a (+) then it is a min. Remember this can be seen by the slope of the graph. This is called the first derivative test... however there is a problem with it that you must always have in the back of your mind. It is only true with continuous functions as Robin "Beans" Wilder pointed out to us.

Next we went on with more examples...

Find the extreme values of f(theta) = tan(theta)
for [-pi/3, pi/4]

F'(theta) = sec^2 = 1/cos^2

There is no points where its zero or undefined so, there are no critical points. Therefore plug is -pi/3 and pi/4.

tan(-pi/3) = -sqrt(3)<------ This is the minimum

tan(pi/4 = 1 <----------- This is the maximum

Here are some links:

http://tutorial.math.lamar.edu/Classes/CalcI/MinMaxValues.aspx

http://www.youtube.com/watch?v=r56mq7iBH4o

http://www.themathpage.com/acalc/max.htm ----- UPDATE

http://library.thinkquest.org/3616/Calc/S2/FMME.html ----- UPDATE

Related Rates Warm up

Mr. O'Brien graduated from Camden-Rockport High School in 1990. How would you do on his AP Calculus exam? Let's try Question 4!

November 17th Blog Post

Click here to see my link.

Related Rates Warm-up and Assignment

Related Rates Warm-up and Assignment

November 15th - Scribe Post

I hope this works, I wasn't sure how to go about using google docs with a scribe post, but i tried it.

here's the post


https://docs.google.com/document/d/14BA-d-Tc76M-fJO0gbp9wxdNk4sOr7cDDRpqgUQ8doQ/edit?hl=en&authkey=CIH9muwK try this one

Novembah 12th's Blog Post

Our class today started off by our class splitting up into little groups to answer the first 3 questions of a worksheet with a mysterious method on it: "Newton's Method". We spent a few moments trying to work it out in small groups. I personally had no idea even where to begin, which is great considering I am writing this blog post.

It all really centers around roots. The root can be thought of as any x-value in a function that will produce a result of zero.

But what is really important about today is the concept of Newton's Method, or the method of approximating the roots in a function.

The process of the method is as follows:

1. Start with an initial guess that is close to the actual root.

2. Find the function's tangent line. Treat this as an approximation of the function itself.

3. Find the x-intercept of the tangent line. This will (generally!) be a better approximation than the one you guessed in STEP 1.

4. Rinse and repeat to get even better approximations.

Here is a nice little visual of these steps. It also happens to be in German. But just in case you're really bad at translation (REALLY BAD), "Funktion" refers to the blue function, and "Tangente" refers to the red tangent lines. It also happened to be created by Ralf Pfeifer, who may or may not be a talented Ju-Jitsu Fighter.

Finally, we found each of the equations for finding the roots.

We started with wanting to find in terms of .

Now, since the slope of a function (in this case f(x)) is its derivative, we can call the slope of the function f'(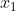). And since 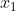is the point we are trying to find, we can define the point as (x, f()).

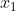By inputting this into point-slope form and by plugging in our x-intercept at (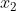, 0) into the equation of the tangent line, I can solve the equation for .

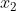Now inputting the x-intercept:

To find , do the same process.

A very cool visual on using Newton's Method is found here.

THIS LINK is actually very cool. It essentially completes Newton's method for you. Just type in your equation, and then your guess for the first root of the function, and it will instantly find x1, x2, x3, and all the way up to x9!

AND FINALLY Oh Lawdy! In case you still don't quite really understand this stuff, this guy is THE MAN. He really clearly explains WHAT Newton's Method is, its point, and why it exists! This video in fact really helped me write this blog post! His voice is really high, and he uses excessive amounts of sound effects. But hey, he's trying!

IN FACT!!! (For review on ANYTHING in CALCULUS we've done so far) please take a look at this link. It is done by the same guy, but reviews ALL of essentially our first semester in under 20 minutes. And it's incredibly entertaining. It really allows you to understand the connections between everything, and it clears up everything!

Happy Trails!

Newton's Method

Today's investigation

november 2, 2010 :)

https://docs1.google.com/document/edit?id=12FYDYFD9MDjscRCxVyqxPkPYuzInMDFP9JTulYUW2fg&hl=en#

October 29, 2010

To start class, we corrected Quiz #4. We collectively did poorly enough on it that it will not be counted towards our grade unless we so choose. Mr. O’Brien noticed that some of us had trouble using the space provided, but he said that the lack of space was intentional. We will get plenty of room to convey our calculations on the AP Test, but if we can work in minimal space, our organization will benefit in plenty of space. Remember to stay as organized and as concise as you can.

During our pretty extensive correcting session, we also decided that besides knowing that and .

To check on our progress with Part 2 of the exploratory, we did some work with logarithm functions and their inverses in Geogebra.

So, our function was which looks like this when graphed:

Note the two points on the graph... (1,5) and (3,6). The first point can be found by taking . Remember that is the same as saying "What power do you raise 3 to to get 1?" Any number raised to zero is 1 so the log (at any base) of one is always zero. 0+5 is 5, so we have the first point. Doing the same thing, (what power do you raise 3 to to get 3?), you find the point (3,6).

Now, to graph the inverse function, we'll use our set of steps...

1. Replace f(x) with y

2. Replace the Ys with Xs and vice versa.

3. Solve for y.

If you work through it, When we graph it, we already know two points on the graph. When graphed, the inverse of a function looks like the graph of the original reflected across the line y=x, so when we reverse the x and y values of the points on f(x) we get points: (6,3) and (5,1) on g(x).

To make sure we knew how to find the derivative of a logarithm, we next found the derivate of f(x) at point (3,6).

so,

and, at the value of x=3.

Note: On the calculator portion of an exam, you can hit "2nd-->trace" to get to the calc function, then hit "dy/dx" for a quick deriv. value.

So, now we know a point on the line, and the slope at that particular point, so we know the equation for the line. Surely enough when graphed, the line is tangent to the function.

For the line tangent to g(x) at (6,3), we have two options. One is to use the derivative rule for exponents, but the other way is far simpler. We know that f(x) and g(x) are inverses of each other, so we know that the two inverse points have reciprocal slopes. Therefore the equation of line tangent to g(x) at (6,3), is .

So, with our various derivative rules, we had only one kind of function we could not take the derivative of: Inverse Trig Functions.

As some background information, we discussed that the inverse functions only exist in certain quadrants of the unit circle. Arcsin and arctan exist in quadrants four and one, while the arccos function, exists in the first and second quadrants. We also discussed that trig functions equal ratios (like ) while inverse trig functions equal angles (like 45 degrees). For a quick review of important inverse trigonometric info, here's some help from wolframalpha:

http://www.wolframalpha.com/input/?i=arcsin

http://www.wolframalpha.com/input/?i=arccos

http://www.wolframalpha.com/input/?i=arctan

Using the example problem cos(arcsin(1/4)), we remembered how to compose trigonometric functions. We know that arcsin is an angle, so we can say that: and therefore . This is where our trigonometric properties from last year come in handy. Remember that ? Well, it does, so we can use it to find cos(arcsin(1\4)). so, . Solve for cosine of the angle, and we get: .

Using this very tactic, we finally have everything we need to solve for the derivatives of inverse trigonometric functions...

In class, we started with y=arcsin(x), which we know is the same as sin(y)=x. Take the derivative with respect to x, and we get: or . Now, we can solve for cos(y) since we know that . We've already stated that sin(y)=x so, , and . Plug that back in for cos(y) in our derivative equation and we have the following rule:

Amazingly, it took implicit differentiation, the chain rule, and trigonometric rules to find the derivative of arcsin. For arccos, we went through a similar process:

so...

Two down...

And that's when we ran out of time... tune in next time for how to find the derivative of arctan... (or just look on http://www.wolframalpha.com/input/?i=derivative+of+arctan). Hint... it has to do with a certain other trigonometric rule...

The next scribe is Julia.