9/9/10 To Infinity and Beyond!

Today, we began class with the very first quiz of the year! Personally, I was a little nervous because it was not like the quizzes we took last year where every question came straight off the homework. However, while taking it, I realized that the questions, while they were not identical, were very similar to those we had done in the homework, and were at the same level of math. This was definitely reassuring as we head into a year of AP Calc! After finishing the quiz, we looked at a practice problem Mr. O'Brien had put on the board. The problem read:

and asked us to first sketch the graph of 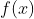then find

and
. Later on, he also asked us to find:




and
So I might as well include those now. Most of us were a little rusty on how to factor, so we started off by factoring, as none of us could instantly pull the graph of the function right off the top of our heads. The easiest thing to do first is to factor the numerator, then the denominator, then to cancel:


By factoring the numerator, we can see that it equals:


which is simple algebra two.
The denominator is a little harder to factor, but it can be done by grouping:
is broken down by grouping by removing an x squared from the first pair of two and a negative four from the second pair of two. You are left with this:

which can be paired into:

or


Upon combining the numerator and denominator, you are left with the equation:


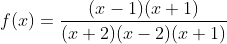
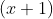
and it becomes clear that the s cancel with one another, which will leave a hole in the graph (remember, we are factoring so we can graph).
This leaves us with the equation:
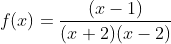
as long as because we removed this variable from the equation in the previous step.
This equation can also be factored using synthetic division. If you need a review, like I did, the Purple Math link was quite helpful.

Now that the equation was simplified, we could FINALLY graph it. Because of the factors in the denominator, it is clear that there are asymptotes at -2 and 2, a zero at 1 (which we know because of the factor in the numerator), and a hole at -1 (which we found earlier). This left us with a pretty good idea of what the graph was going to look like, and the only thing we still had to find was the end behavior. To do this, we used a "funny form" of the highest power of x, taken from the original graph,

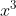
Clearly, the highest power of x is , so we multiply the numerator and the denominator by (which is okay because it is just another form of one) to factor down the graph and see what it will look like as x gets infinitely larger. When multiplying by this FUFOO, we wind up with the expression:

(On a side note, it is really complicated to enter that into the equation editor)
By pretending that x is a huge number, we are able to see whether the equation is getting infinitely larger or smaller by "substituting" it in and deciding whether it grows large, or grows close to zero. By doing this "substitution", we see the following:

or simplified:
.
This means that the end behavior goes to zero because, as x gets infinitely large, f(x) gets smaller and smaller.

We are finally ready to graph, and get a graph that looks like this:

The pink dotted lines are the vertical asymptotes, and the orange dot is the hole.

Now that we have a graph, it is easy to figure out what the limits are.

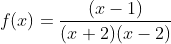
is , which we know because of where the hole is (if you do plug -1 into the equation , you will get ).

does not exist (DNE) because we know that there is a vertical asymptote at 2, so there is obviously no limit.

does exist, because, as long as you specify which side you are approaching a limit from, you can have a limit for that one side (for another example of this look at homework problem 13 on page 72). By looking at the graph, we are able to see that the limit is
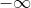
because the limit goes down the asymptote, and the asymptote goes on for infinity.

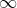
equals , as it runs alongside the positive end of a vertical asymptote.

equals 0, which we discovered when we were figuring out the end behaviors of the function.

After doing this problem, we moved onto more examples to demonstrate further limits of infinity.
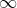
Our first practice problem was . In this problem, the limit is because, as you subtract the 4 from a number very close to it (like 4.00001), the denominator is a very tiny decimal. 7 divided by a tiny (but positive) number is infinity.

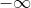
Next, we found , and discovered that the limit was because, although you use the exact same process and reasoning as the above example, the denominator is left negative, which makes that whole fraction negative.

Our next example was slightly more complex:

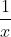
To begin, we multiplied by a FUFOO of to get:
And using our reasoning from earlier, we know that if x gets infinitely large, then the fractions cancel to zero, leaving us with . A video of this problem is below:


Another sample problem we did was
. Again, we multiplied by a FUFOO of , and the function became the expression:
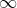
. When x would get infinitely large, the fractions in the denominator would get very close to zero. One divided by a tiny number is , so the limit to the function is also .

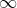
The FINAL practice problem of the day involved a swinging pendulum that swung at the equation . This equation had a pretty cool graph (like a sideways tornado), but the graph is actually irrelevant in doing this problem! The first thing Mr. O'Brien asked us to do was to find the limit when the function approached infinity. Upon analyzing the function, we realized that it was an exponential decay function because of the . This means that everything from the 30 right of the equation cancels to zero as t gets exponentially larger, so the limit is 50. Although the limit is 50, the equation itself does not have to go to 50, as the limit and d(t) are unrelated.

We did a bunch of practice problems in class today and learned much more about limits! We even pulled some of our precalc out of the closet and began to dust the cobwebs off! If you still need more of an explanation, here are some practice problems with explanations. There are 19 of them, so that should be plenty:
http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/liminfdirectory/LimitInfinity.html

UPDATE:
This link makes limits that approach infinity super easy to understand!
http://www.mathsisfun.com/calculus/limits-infinity.html

Homework:
-Make sure assignments 1,2, and 3 are checked and ready to be given to Mr. O'Brien. No waiting to do homework until the day before the test this year!
-Assignment #4: p. 81/1, 3, 7, 9, 11, 21, 27, 29, 31, 45, 47, 53, 57, 61