That is, it started half past nine



For an added bonus, here's some algebra:

And we quizzed ourselves until 10:10
Using rules and signs and sines.
We then went over Kyle's post
A great job that he did
This lasted till 10:45
And then we worked derivs
We did Implicit chain rule
Until our brains did drool
And now I'm up at 3 o'clock
Because of this stupid school.
The first problem we faced was the infamous
This evil little guy sparked a flew of mathematical steps:
(NOTE that the derivative of y is not 1 in this case because it is the value we are trying to find)
Now, using the glorious product rule, we can make this little function more complicated:
Now, we know from the Power Rule that x' equals 1. So,
And using our awesome Algebra I skills which we all CLEARLY remember, if we move all of the y' to one side of the equation then we will be able to find out what y' equals:
Now if I pull out the y', I can isolate it:
LOOK AT THAT BEAUTIFUL ANSWER! It's a prettycool formula, that Implicit Differentiation. Yep.
So then we took a look at a few homework questions: Namely pg 174 #19 and #35b. If you want me to write these up, I'll do it over the weekend. But for now, you have the back of your book!
Finally, we took a look at inverses.
There are a few simple steps to find the inverse of a function:
1. Switch your x and y values. EX. y=3x would now be x=3y.
2. Isolate your "y" value. EX. in x=3y, to find y, I'd have to divide the x by 3. y=x/3.
So, like in STEP 1, we switch the y and x values:
Then solve:
So, for the original function 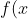=x^{3}+1) , we now have an inverse of
, we now have an inverse of ![f^{-1}(x)=\sqrt[3]{x-1}](http://latex.codecogs.com/gif.latex?f^{-1}(x)=\sqrt[3]{x-1}) . This is what this looks like graphically:
. This is what this looks like graphically:

Now, I can take the same point on each function to see what relationship exists between a derivative and an inverse. I chose the points (1,2) for f(x) and (2,1) for g(x).

First I need to find the derivative (or the slope) to find the tangent line at point A. So, if I take  and Power Rule all over it, then I get
and Power Rule all over it, then I get 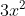 . At f(1), the slope is 3. If I then input this into Point-Slope formula, I get
. At f(1), the slope is 3. If I then input this into Point-Slope formula, I get
which equals
The derivative (or slope, again) of g(x) must be found!
Now to nab the derivative using the Chain Rule:
Now to input the "x" of my point. In this case it would be "2".
Yay! So now that we know the slope of the new derivative, I can input it, once again, into point-slope form.
The derivatives are perfect reciprocals of each other!
Now, let's take a final look at them graphically to just get an eye to what this looks like:
NOTE: h(x) and k(x) are the tangent lines.

Look at those colors! Those tangent slopes are perfect reciprocals!
PROVE:
The derivatives of inverse functions are reciprocals.
PROOF:
Let f(x) and g(x) be inverse functions to each other.
Now I can take the derivs of both sides:
Q.E.D.
Another example:
Let's freaking graph it!

NOTE: The function is cut off at x≥1 because it was a whole cubic function, then it wouldn't pass the horizontal line test. This type of function is called a 1 to 1 function.
Inverse: (3,??)
Original: (??,3)
So now because I know I will be using the value "3", I can set my function equal to it:
Now that it is set to 0, I can synthetically divide. The divisor is positive 2, which results in the function equaling (2x^{2}+x+2)) . AAAAAAAAAAND that's as far as we got in class.
. AAAAAAAAAAND that's as far as we got in class.
Anyways, if you need any help with finding the derivatives of inverse functions, click here. It does have some bits that we haven't covered yet, but ignore that.
This one is very similar to the stuff we've been doing.
And these guys are pretty awesome too :D
I thought I might add another link! *update*
Well, it's 3. I'll probably be grumpy tomorrow due to lack of sleep. Hello, Friday.
The next scribe post WILL NOT be anyone in the musical, because they would keel over more than I already am doing. So, I'm sorry, Marcel, but you're not involved in the musical and it's been a little while. Enjoy!
So, first I run across this on my Facebook:
ReplyDeletehttp://www.youtube.com/watch?v=ngi8FEI4j_c
Then, I read this post. Seriously, is there anything Andy doesn't do exceptionally well?!?