Novembah 12th's Blog Post

Our class today started off by our class splitting up into little groups to answer the first 3 questions of a worksheet with a mysterious method on it: "Newton's Method". We spent a few moments trying to work it out in small groups. I personally had no idea even where to begin, which is great considering I am writing this blog post.

It all really centers around roots. The root can be thought of as any x-value in a function that will produce a result of zero.

But what is really important about today is the concept of Newton's Method, or the method of approximating the roots in a function.

The process of the method is as follows:

1. Start with an initial guess that is close to the actual root.

2. Find the function's tangent line. Treat this as an approximation of the function itself.

3. Find the x-intercept of the tangent line. This will (generally!) be a better approximation than the one you guessed in STEP 1.

4. Rinse and repeat to get even better approximations.

Here is a nice little visual of these steps. It also happens to be in German. But just in case you're really bad at translation (REALLY BAD), "Funktion" refers to the blue function, and "Tangente" refers to the red tangent lines. It also happened to be created by Ralf Pfeifer, who may or may not be a talented Ju-Jitsu Fighter.

Finally, we found each of the equations for finding the roots.

We started with wanting to find in terms of .

Now, since the slope of a function (in this case f(x)) is its derivative, we can call the slope of the function f'(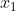). And since 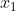is the point we are trying to find, we can define the point as (x, f()).

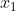By inputting this into point-slope form and by plugging in our x-intercept at (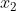, 0) into the equation of the tangent line, I can solve the equation for .

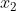Now inputting the x-intercept:

To find , do the same process.

A very cool visual on using Newton's Method is found here.

THIS LINK is actually very cool. It essentially completes Newton's method for you. Just type in your equation, and then your guess for the first root of the function, and it will instantly find x1, x2, x3, and all the way up to x9!

AND FINALLY Oh Lawdy! In case you still don't quite really understand this stuff, this guy is THE MAN. He really clearly explains WHAT Newton's Method is, its point, and why it exists! This video in fact really helped me write this blog post! His voice is really high, and he uses excessive amounts of sound effects. But hey, he's trying!

IN FACT!!! (For review on ANYTHING in CALCULUS we've done so far) please take a look at this link. It is done by the same guy, but reviews ALL of essentially our first semester in under 20 minutes. And it's incredibly entertaining. It really allows you to understand the connections between everything, and it clears up everything!

Happy Trails!